红黑树

红黑树规则

红黑树和平衡二叉树一样，都是一种自平衡的二叉树，且红黑树有它自己的规则：

1. 每个节点都有颜色，红色或黑色
2. 根节点是黑色
3. 叶子节点是黑色，且是NIL
4. 两个红色节点不能相连
5. 每个节点到叶子节点(NIL)的路径上，黑色节点的数量都一样

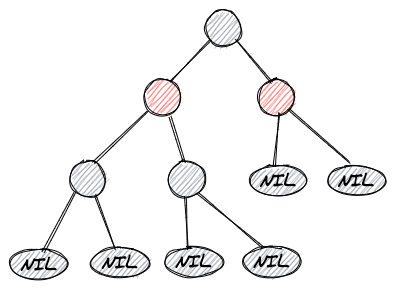
说起来有点抽象，下图是一棵红黑树的示例：

红黑树中，最长路径不会超过最短路径的2倍，为什么呢？

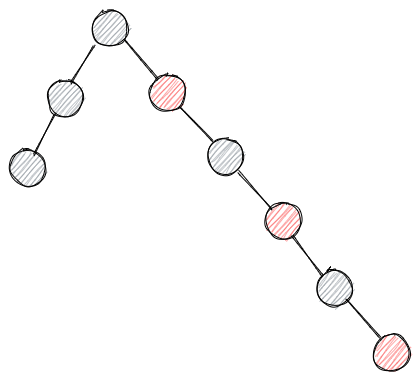
在红黑树中，最短路径是全是黑色节点的路径，而最长路径是红黑交替的路径。

根据红黑树的规则，每个路径上黑色节点数量必须一致，因此最长路径最多是最短路径的2倍，如下图

插入新节点

当红黑树插入后删除节点时，红黑树可能失衡，此时则需要通过变更节点颜色和左旋右旋让红黑树恢复平衡。

新插入的节点的颜色可以是红色或黑色，但是红黑树规则中，任一路径上的黑色节点数量是相同的，为了不破坏这个规则，因此我们新插入一般都定为红色

红黑树的左旋与右旋是和平衡二叉树一模一样的，参考 平衡二叉树(AVL)

当插入节点后没有破坏红黑树的规则，那么则无需变动。若破坏了规则，则需要变色或旋转。

从某网看到一个顺口溜，可以参考一下：

根节点必黑，新增是红色，只能黑连黑，不能红连红；

爸叔通红就变色，爸红叔黑就旋转，哪边黑往哪边转

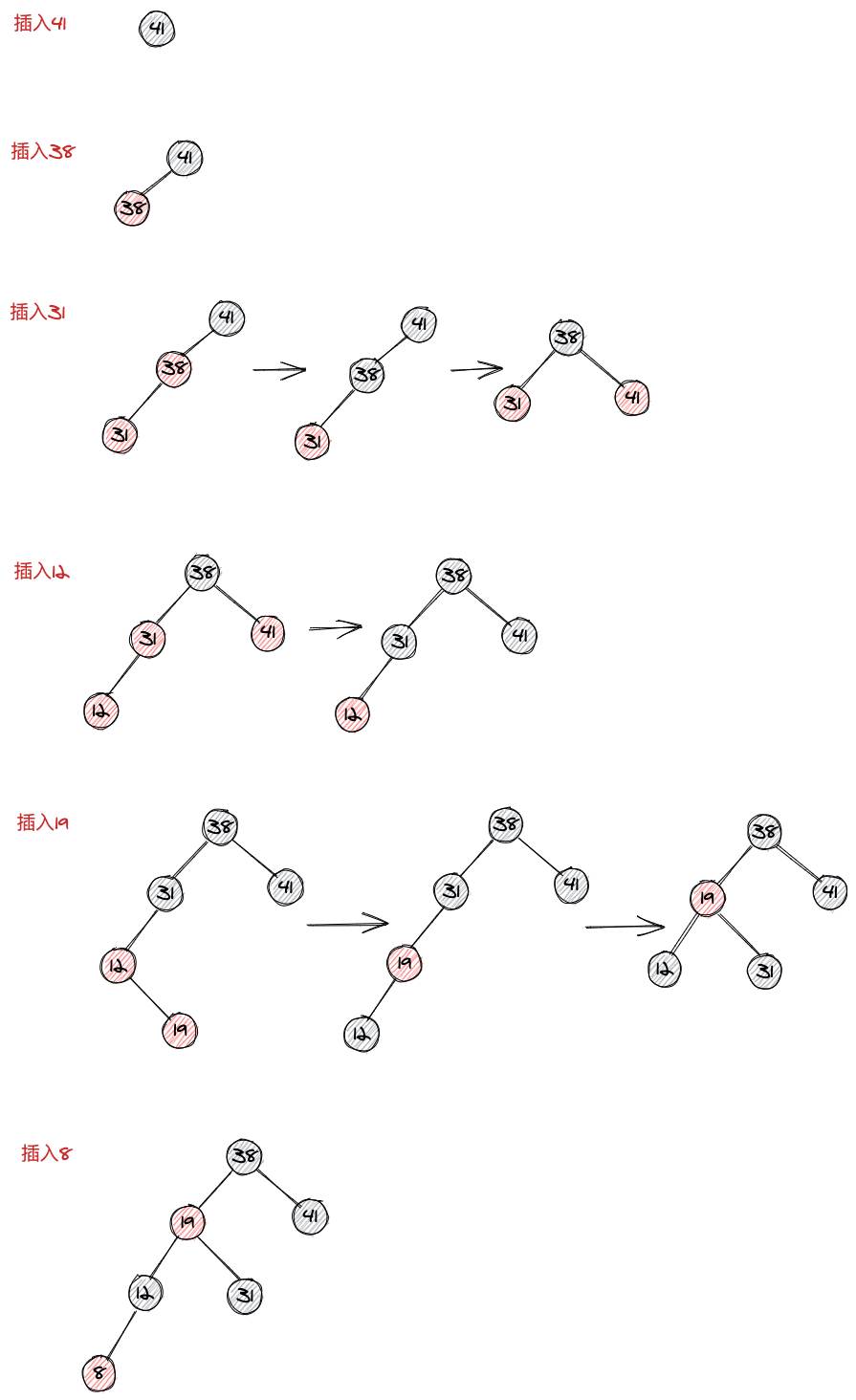
根据这个顺口溜，做点练习题

41、38、31、12、19、8 连续地插入一棵初始化为空的红黑树之后，画出该结果树